Descubre como determinar la masa de una estrella

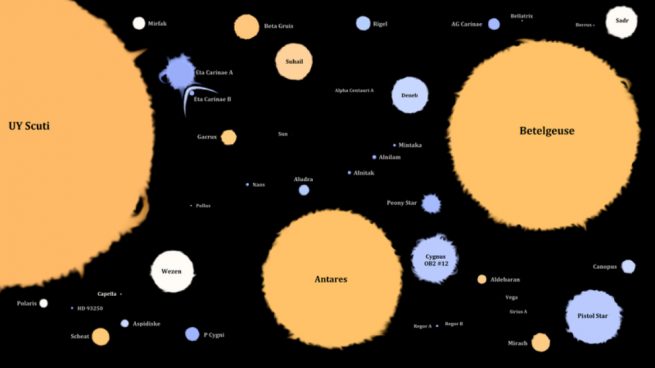
Casi todo en el universo tiene masa , desde átomos y partículas subatómicas hasta cúmulos gigantes de galaxias. En este caso, os explicamos, cómo determinar la masa de una estrella.

Es importante conocer  la masa, pero los objetos en el cielo están demasiado distantes. No podemos tocarlos y ciertamente no podemos pesarlos por medios convencionales. Entonces, ¿cómo determinan los astrónomos la masa de las cosas en el cosmos?.

Cómo medir la masa de una estrella

La masa de una estrella, la cantidad de material que contiene, es una de sus características más importantes. Si conocemos la masa de una estrella, como veremos, podemos estimar cuánto tiempo brillará y cuál será su destino final. Sin embargo, la masa de una estrella es muy difícil de medir directamente. De alguna manera, necesitamos poner una estrella en el equivalente cósmico de una escala.

Afortunadamente, no todas las estrellas viven como el Sol, aisladas de otras estrellas. Aproximadamente la mitad de las estrellas son estrellas binarias, dos estrellas que orbitan entre sí, unidas por la gravedad. Las masas de estrellas binarias se pueden calcular a partir de las mediciones de sus órbitas, al igual que la masa del Sol se puede obtener midiendo las órbitas de los planetas a su alrededor.

Medir la masa de estrellas en sistemas binarios es fácil. Como hemos mencionado, los sistemas binarios son conjuntos de dos o más estrellas en órbita entre sí. Al medir el tamaño de la órbita, las velocidades orbitales de las estrellas y sus períodos orbitales, podemos determinar exactamente cuáles son las masas de las estrellas. Podemos tomar ese conocimiento y luego aplicarlo a estrellas similares que no están en múltiples sistemas.

También podemos medir fácilmente la luminosidad y la temperatura de cualquier estrella. Un diagrama de luminosidad versus temperatura para un conjunto de estrellas se llama diagrama de Hertzsprung-Russell (HR), y resulta que la mayoría de las estrellas se encuentran a lo largo de una banda delgada en este diagrama conocida como la secuencia principal. Las estrellas se organizan en masa en la secuencia principal, con estrellas masivas que son más calientes y brillantes que sus hermanos de masas pequeñas. Si una estrella cae en la secuencia principal, por lo tanto, sabemos de inmediato su masa.

Además de estos métodos, también tenemos una excelente comprensión de cómo funcionan las estrellas. Nuestros modelos de estructura estelar son excelentes predictores de las propiedades y la evolución de las estrellas. Como resultado, la masa de una estrella determina su historia de vida desde el día 1, para todos los tiempos posteriores, no solo cuando la estrella está en la secuencia principal. Entonces, en realidad, la posición de una estrella en el diagrama HR es un buen indicador de su masa, independientemente de si está en la secuencia principal o no.

Medir la masa de una estrella con la tercera ley de Kepler

Con la ayuda de la forma exacta de la tercera ley de Kepler, también se puede determinar la suma de las masas de los dos componentes de un sistema estelar binario a partir de la gran semiaxis de la órbita verdadera relativa a y el tiempo orbital T:

Esta es la fórmula:

• m1 + m2 = 4Pi ^ 2 / G * a ^ 3 / T ^ 2

En la que: 

• a = gran semiaxis de la órbita verdadera relativa
• T = período orbital
• G = constante gravitacional
• m 1 , m 2 = masas de los dos componentes

La fórmula superior requiere el gran semiaxis de la órbita verdadera relativa en metros, el tiempo orbital en segundos y da la suma de la masa en kg. Esto conduce a valores algo difíciles de manejar (grandes). Si realizas algunas transformaciones, también puede usar unidades más «prácticas». Entonces obtienes:

• (m 1 + m 2 ) = (a 3 * r 3) / T 2

En la que: 

• a = semieje mayor de la órbita verdadera relativa en segundos de arco
• r = distancia del sistema en parsec
• T = período orbital en años
• m 1 , m 2 = masas de los dos componentes en masas solares

Si los grandes semiejes a 1 y 2 de las rutas absolutas también se conocen, entonces se puede calcular la relación de masa:

• m 1 / m 2 = a 2 / a 1

En la que:

•  m 1 , m 2 = masas de los dos componentes
• a 1 , a 2 = semiejes grandes de las rutas absolutas

Con la suma de masa (m 1 + m 2 ) y la relación de masa (m 1 / m 2 ) es posible calcular las masas de los dos componentes.