Casi nadie lo resuelve: el acertijo visual que sólo aciertan los que se fijan en este detalle
¿Eres capaz de resolverlo?
El acertijo visual que te traerá de cabeza: ¿Sabrías decir cuántas personas están acampando?
El acertijo visual que te ayuda a descubrir tu nivel de inteligencia: ¿eres capaz de resolverlo?
Parece Cinque Terre pero este pueblo con fachadas de colores está en España y es un sueño
Ni Filipinas ni Cuba: el único país que volvió a ser de España tras su independencia
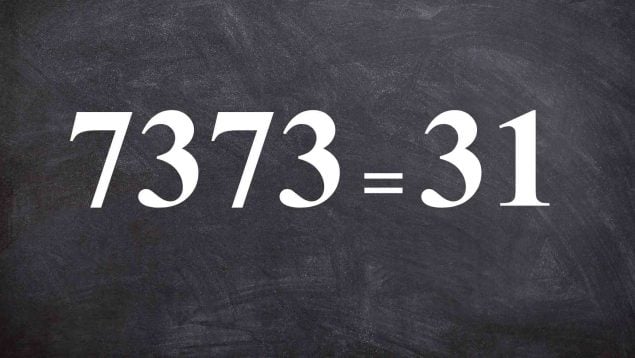

Los acertijos visuales y matemáticos son más que simples pasatiempos; son herramientas efectivas para el desarrollo cognitivo. Enfrentarse a estos desafíos no sólo es divertido, sino que también potencia habilidades clave que se pueden aplicar en la vida tanto personal como profesional. Uno de los beneficios más significativos es la estimulación del pensamiento lógico, que se logra al estructurar el pensamiento de manera clara y secuencial. Además, la resolución de un acertijo visual mejora la concentración, ya que muchas soluciones dependen de detalles sutiles que requieren atención.
Asimismo, estos acertijos promueven el desarrollo de la resolución de problemas, alentar a los participantes a considerar diferentes enfoques ante desafíos únicos. Esta flexibilidad en el pensamiento es crucial en un entorno donde los problemas complejos son comunes. Por otro lado, al buscar soluciones innovadoras, se estimula la creatividad, lo que resulta valioso en el ámbito laboral. Finalmente, la práctica regular fortalece la memoria, ya que recordar patrones y estrategias previas mejora la retención de información. En conjunto, resolver acertijos visuales y matemáticos no sólo entretiene, sino que también se convierte en una herramienta potente para desarrollar habilidades esenciales en diversas áreas de la vida.
El acertijo visual que se ha hecho viral
¿Crees que tienes el ingenio matemático para resolver un acertijo visual que está causando furor en Internet? Te presentamos un desafío intrigante con cuatro números: 7, 3, 7 y 3, que se relacionan con un resultado final de 31 a través de operaciones matemáticas. Este enigma pone a prueba no sólo tus habilidades de cálculo, sino también tu lógica y creatividad. Mientras intentas descubrir la solución, tu mente se activa y conecta diferentes conceptos matemáticos, fomentando un pensamiento crítico esencial.
Para abordar este acertijo visual, es fundamental seguir un proceso claro. Primero, multiplicamos el primer 7 por el primer 3, lo que nos da 21. Este paso inicial sienta las bases para el resultado final. Luego, sumamos los otros dos números, 7 y 3, cuyo resultado es 10. Este segundo paso es clave para entender cómo los diferentes elementos del acertijo se combinan. Finalmente, unimos ambos resultados: 21 y 10, para llegar a la suma total de 31.
Así que la operación que resuelve este enigma es: (7×3)+(7+3)=31(7×3)+(7+3)=31. Te animamos a compartir este reto con amigos y familiares para ver quién puede encontrar la solución más rápido. Sin duda, es una excelente forma de poner a prueba y afinar tus destrezas matemáticas, al tiempo que disfrutas de un rato de entretenimiento y diversión.
Los mayores enigmas matemáticos de la historia
El Último Teorema de Fermat, propuesto por Pierre de Fermat en 1637, establece que no existen tres números enteros positivos \(a\), \(b\) y \(c\) que satisfagan la ecuación \(a^n + b^n = c^n\) para \(n > 2\). Aunque Fermat dejó una nota sobre una “prueba maravillosa”, la conjetura permaneció sin solución durante más de 350 años. En 1994, el matemático británico Andrew Wiles logró demostrar el teorema utilizando técnicas avanzadas de teoría de números y geometría algebraica, marcando un hito en la historia de las matemáticas y mostrando la interconexión entre diferentes áreas matemáticas.
La Hipótesis de Riemann, propuesta por Bernhard Riemann en 1859, aborda la distribución de los números primos y postula que todos los ceros no triviales de la función zeta de Riemann tienen parte real igual a 1/21/2. Esta conjetura es crucial para comprender cómo se distribuyen los números primos y tiene implicaciones significativas en varias áreas de la matemática. A pesar de su claridad, ha permanecido sin prueba durante más de 160 años, convirtiéndose en uno de los problemas más desafiantes. Su resolución podría ofrecer insights sobre la teoría de números y afectar campos como la criptografía y la teoría de sistemas complejos.
La Conjetura de Collatz, o problema 3n+13n+1, plantea una secuencia simple de operaciones en números enteros positivos. Se empieza con un número entero: si es par, se divide entre 2; si es impar, se multiplica por 3 y se suma 1. La conjetura sugiere que, sin importar el número inicial, esta secuencia siempre llegará a 1. Desde su formulación en 1937 por Lothar Collatz, ha sido verificada para millones de números, pero sigue sin encontrarse una prueba genera. Este enigma ilustra cómo problemas aparentemente simples pueden ocultar complejidades profundas.
El Problema de los Cuatro Colores, formulado por Francis Guthrie en 1852, aborda la coloración de mapas, afirmando que sólo se necesitan cuatro colores para que no haya regiones adyacentes del mismo color. Aunque esta idea parece intuitiva, la prueba resultó ser compleja y evasiva para los matemáticos durante más de un siglo. En 1976, Kenneth Appel y Wolfgang Haken lograron demostrar la conjetura utilizando una combinación de razonamiento matemático y computación, marcando un hito como uno de los primeros casos en que una computadora contribuyó a una prueba matemática. Sin embargo, esto generó controversia sobre la validez de las pruebas computacionales, ya que su longitud y complejidad dificultaban su verificación manual. El Problema de los Cuatro Colores se considera un caso emblemático en teoría de grafos y geometría combinatoria.









