Cómo hacer un rectángulo áureo
Para hacer un rectángulo áureo tienes que tener en cuenta la llamada proporción áurea que es aproximadamente 1:1,618
No necesitas secadora: el truco más efectivo para secar la ropa en la lavadora usando sólo una toalla
El truco del papel de aluminio con el que van a desaparecer los odiosos pelos de tu ropa si tienes mascota
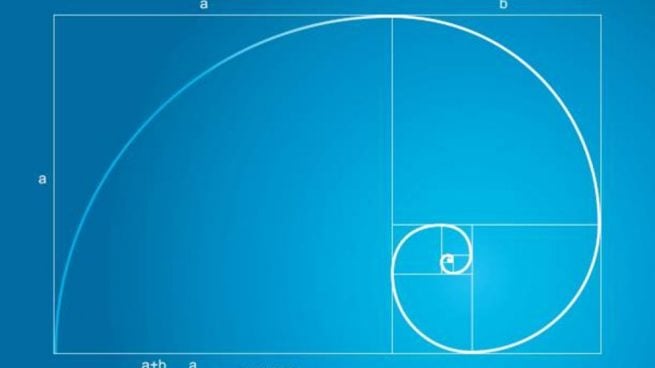
Ya sea para un trabajo de arquitectura, de diseño o también como parte de una clase de álgebra, quizás necesites hacer un rectángulo áureo que siempre está basado en la llamada «proporción áurea», la cuál se da en mucha de las formas más armoniosas de la naturaleza. Veamos a continuación paso a paso y de forma fácil, Cómo hacer un rectángulo áureo.
Para hacer un rectángulo áureo, tendremos que tener en cuenta la mencionada proporción áurea, que es la relación entre la longitud y el ancho de la que se dice que es una de las formas rectangulares más estéticamente agradables. Este rectángulo, llamado Rectángulo Áureo, aparece en la naturaleza y es utilizado por los seres humanos tanto en el arte como en la arquitectura. La proporción áurea se puede observar en la forma en que crecen los árboles, en las proporciones de cuerpos humanos y animales. La proporción está cerca del número 1.618 o de hecho en la escala 1:1,618. Descubrir este tipo de proporción es algo realmente maravilloso, pero nosotros mismos podemos recrearla a través del rectángulo áureo, algo que seguramente te van a pedir a la hora de crear un diseño de arquitectura, o de cualquier pieza de diseño que tenga que tener una proporción que sea muy específica.
Pasos para hacer un rectángulo áureo
En el caso de que te hayan pedido que realices un rectángulo áureo, tienes que encontrar primero la proporción áurea. Para ello, puedes considerar un segmento de línea de una longitud x + 1 tal que la relación del segmento de línea completo x + 1 al segmento más largo x sea la misma que la relación del segmento de línea, x, al segmento más corto, 1.
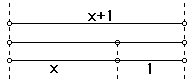
Así,
![]()
La ecuación cuadrática resultante es
![]()
Una raíz positiva de esta ecuación sería entonces
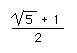
o 1.61803 … Este es su número irracional, o su recíproco
![]()
Esto es conocido como el Ratio áureo o phi .
Ahora construiremos el Rectángulo Dorado. Primero construiremos un cuadrado ABCD.
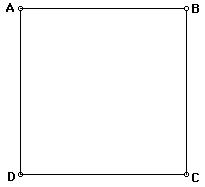
Ahora construiremos el punto medio E de DC.
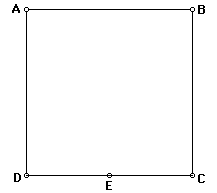
El siguiente paso será extender DC. Con el centro E y el radio EB, dibuja un arco que cruce EC extendido en C.
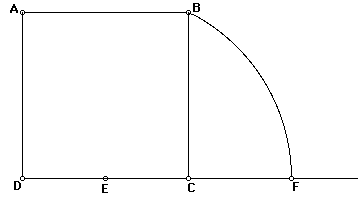
A continuación, construye un perpendicular a DF en F.
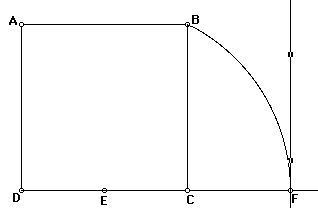
Extiende AB para intersectar la perpendicular en G.
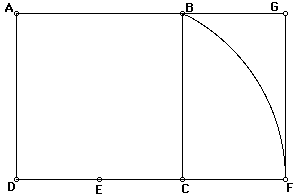
AGFD es ya un rectángulo áureo
Ahora vamos a medir la longitud y el ancho del rectángulo. Luego encontraremos la relación entre la longitud y el ancho. Esto debería estar cerca de la proporción áurea (aproximadamente 1.618).
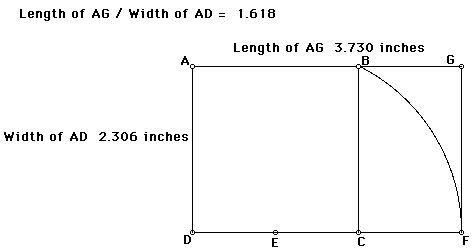
Ahora tomaremos nuestro Rectángulo áureo y continuaremos dividiéndolo en otros Rectángulos áureos.
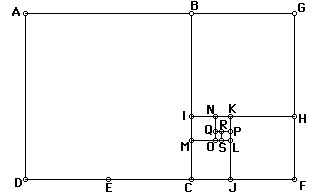
Dentro de este gran rectángulo áureo hay otros seis rectángulos áureos.
Cuando midas la longitud y el ancho de cada rectángulo áureo, verás que la relación entre la longitud y el ancho es la proporción áuarea (aproximadamente 1.618).
Ahora construiremos la espiral a través de todo el Rectángulo áureo, uniendo los puntos: D,B,H, J, M, N, P, S y R.
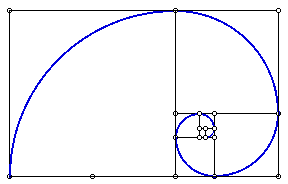
Temas:
- Diseño
- Matemáticas









