Qué es el sistema hexadecimal, para qué sirve y ejemplos
El sistema hexadecimal es un método de numeración posicional que utiliza como base el número 16
Como pasar de binario a decimal
Cómo pasar de decimal a binario paso a paso y fácilmente
Hipótesis Némesis: ¿Es el Sistema Solar un sistema binario?
Descubre como determinar la masa de una estrella

Qué es el sistema hexadecimal, para qué sirve y ejemplos. Mientras que el sistema decimal con sus diez dígitos es parte integral e nuestra vida diaria normal, la informática y el procesamiento de datos se basan en el sistema binario o código binario . Esto nos permite representar problemas complejos con solo dos estados: 0 y 1. Sin embargo, los números binarios grandes tienen la desventaja de que a menudo son incomprensibles. En este caso, el sistema hexadecimal brinda un remedio: de hecho, la información que necesitaría 8 dígitos en el sistema binario se puede expresar con solo 2 números hexadecimales.
Qué es el sistema hexadecimal
¿Qué es el sistema hexadecimal? ¿Cuáles son los dígitos de este sistema de numeración y para qué sirve? ¿Se puede cambiar o convertir a otros sistemas numéricos como el sistema decimal o el sistema binario? Resolvamos todas estas dudas y otras en torno al sistema hexadecimal y cómo funciona.
La palabra hexadecimal consta de las palabras hexa y decem . Hexa proviene del griego y significa «seis», mientras que decem es la palabra latina para «diez». Por lo tanto, el sistema hexadecimal es un sistema de valor de posición que representa números sobre una base de 16 dígitos. Esto significa que el sistema numérico hexadecimal usa 16 dígitos diferentes. En otras palabras: hay 16 símbolos de dígitos posibles, contra dos en el sistema binario (1 y 0) y diez en el sistema decimal (0 a 9). Esto significa que el sistema hexadecimal usa 16 símbolos para marcar un número, que son:
- dígitos del 0 al 9 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
- las letras de la A a la F (A, B, C, D, E, F).
El sistema de numeración que usamos todos los días es el sistema decimal (o base diez), que usa los dígitos del 0 al 9 para marcar cualquier número.
Dado que se necesitan 16 símbolos en el sistema hexadecimal , las primeras seis letras mayúsculas del alfabeto (de la A a la F) se agregan a los diez dígitos del sistema decimal para un total de 16 símbolos.
Para indicar que un número está escrito usando el sistema hexadecimal, y así diferenciarlo de las representaciones en otras bases, se debe encerrar entre paréntesis e indicar la base como subíndice (en este caso 16). Cuando se omite la base, significa que el número se expresa en base diez.
Por ejemplo, si escribimos o vemos representado 302, diremos que es el número trescientos dos en el sistema de numeración decimal, mientras que si vemos representado (302) 16, representa un número en el sistema hexadecimal y se lee «tres cero dos en base dieciséis», es decir, los dígitos que lo componen se leen uno a la vez, luego especificando la base.
Este es además un sistema que pertenece a la categoría de sistemas numéricos posicionales, es decir, que cada dígito tiene un valor diferente según la posición que ocupa dentro del número.
Tomemos un ejemplo para aclarar el concepto. El número hexadecimal 4F equivale al número decimal 79. Para evitar confusiones, es recomendable indicar la base del número con un índice en la parte inferior derecha, como vemos en esta imagen:
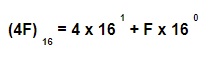
Sabemos que el dígito hexadecimal F es igual al número decimal 15, mientras que el dígito 4 es el mismo para ambos sistemas numéricos. Para calcular el número decimal equivalente del número hexadecimal 4F reescribimos la operación de cálculo solo con valores decimales.
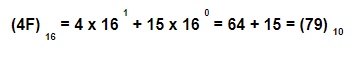
Para qué sirve el sistema hexadecimal
El sistema hexadecimal se utiliza en tecnología informática y facilita la legibilidad de grandes números o largas secuencias de bits . Estos se agrupan por cuatro bits cada uno y se convierten a números hexadecimales. El resultado: largas secuencias de unos y ceros se convierten en números hexadecimales más cortos, que a su vez se pueden dividir en grupos de dos o cuatro. Por lo tanto, los números hexadecimales son una forma más compacta de representación de secuencias de bits. El sistema se utiliza, entre otras cosas, en la dirección de origen y destino del Protocolo de Internet (IP) , en el código ASCII y en la descripción de códigos de color en diseño web en lenguaje CSS .
De este modo, el sistema hexadecimal tiene la ventaja de ocupar una menor cantidad de símbolos (dígitos) para almacenar datos y valores numéricos muy grandes, ya que permite ocupar menos memoria en términos de bytes. El sistema hexadecimal también es particularmente útil ya que cada dígito hexadecimal se puede representar con exactamente cuatro dígitos binarios. Por ejemplo, el último dígito del sistema hexadecimal (F) 16 es igual al número binario (1111) 2.
El sistema hexadecimal: la escritura
Como ya se mencionó, el sistema hexadecimal proporciona 16 símbolos numéricos posibles. Sin embargo, surge un problema potencial: con la notación numérica convencional, los números decimales 10, 11, 12, 13, 14 y 15 se usan usando dos símbolos contiguos. Sin embargo, cuando el número 10 se expresa en notación hexadecimal, no está claro si nos referimos al número decimal 10 o al número binario 2 (1 + 0).
Para resolver este problema, los números hexadecimales que denotan los valores 10 a 15 se reemplazan por las letras mayúsculas A, B, C, D, E y F. Por lo tanto, en el sistema hexadecimal, los números 0 a 9 y las letras mayúsculas de la A a la F se utilizan para representar el equivalente del número binario o decimal. Para distinguir los números hexadecimales de los números decimales, existen diferentes tipos de notación disponibles (en los siguientes ejemplos, se describe el número hexadecimal «73»):
- 7316
- 73hex
- 73h
- 73H
- 73H
- 0x73
- $73
- #73
- «73
- X’73’
El prefijo 0x y el sufijo h se usan especialmente en programación, mientras que el prefijo del signo de dólar se usa con ciertas familias de procesadores de lenguaje ensamblador.
Tabla del sistema hexadecimal
Para facilitar la comprensión del concepto, publicamos a continuación la tabla de los primeros números hexadecimales. Esta es una tabla que enumera los 16 dígitos del sistema hexadecimal y su valor en base 10 y base 2. de modo que nos puede servir como una de las herramientas de conversión más válidas del sistema decimal y binario al sistema hexadecimal, y viceversa.
| Sistema hexadecimal | Sistema decimal | Sistema binario |
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| A | 10 | 1010 |
| B. | 11 | 1011 |
| C. | 12 | 1100 |
| D. | 13 | 1101 |
| E. | 14 | 1110 |
| F. | 15 | 1111 |
Usos y ventaja del sistema hexadecimal
Cualquier dígito hexadecimal de (0) a (F) se puede convertir así en un número décimal o en un número binario de cuatro dígitos. Esta característica de los números hexadecimales facilita el proceso informático de convertir y almacenar números en un dispositivo electrónico, memoria digital y principalmente, en los ordenadores.
Por ello, este formato es muy utilizado en informática porque permite una fácil conversión con el sistema binario que utilizan las computadoras .
Además, la notación hexadecimal es más compacta que la notación binaria y utiliza hasta cuatro veces menos dígitos que la notación binaria para representar el mismo número.
Como ya habréis comprobado con solo mirar la tabla de arriba, la conversión de binario a hexadecimal se realiza agrupando los dígitos ( bits ) cuatro por cuatro, o viceversa reemplazando cada dígito hexadecimal por 4 dígitos binarios. De este modo:
- binario: 1.0101.1010.1010.1100.1111.0111
- agrupados por 4: 1 0101 1010 1010 1100 1111 0111
- agrupados en hexadecimal: 1 5 A A VS F 7
- hexadecimal: 15AACF7
- decimal: 22719735
La conversión con el sistema decimal no presenta ninguna dificultad particular. Por lo tanto, 15AACF7 se convierte calculando:
![]()
El sistema hexadecimal representa para cada dígito exactamente la mitad de un byte . Esta es una ventaja para el uso de la computadora, donde el byte es la unidad de cuenta. Por otro lado, las potencias naturales del sistema hexadecimal corresponden a los prefijos binarios Méga-, Téra-, Exa- y Yotta- (siendo dieciséis elevado a cinco, diez, quince y veinte respectivamente). Los múltiplos binarios intermedios: kilo-, Giga-, Péta- y Zetta- son respectivamente 0x400 unidades, 0x400 Mebi, 0x400 Tebi y 0x400 Exbi.
Por último, la conversión de texto de escritura alfabética a notación hexadecimal se puede lograr utilizando notación ASCII . La letra «A» corresponde así al código hexadecimal 41 y el espacio al código hexadecimal 20.
Temas:
- Matemáticas









